Binary Search Tree (BST)

Binary Search Tree

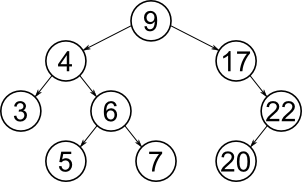
A binary search tree (BST), also known as an ordered binary tree, is a node-based data structure in which each node has no more than two child nodes. Each child must either be a leaf node or the root of another binary search tree. The left sub-tree contains only nodes with keys less than the parent node; the right sub-tree contains only nodes with keys greater than the parent node.

The BST data structure is the basis for a number of highly efficient sorting and searching algorithms, and it can be used to construct more abstract data structures including sets, multisets, and associative arrays. 

Binary search trees keep their keys in sorted order, so that lookup and other operations can use the principle of binary search: when looking for a key in a tree (or a place to insert a new key), they traverse the tree from root to leaf, making comparisons to keys stored in the nodes of the tree and deciding, on the basis of the comparison, to continue searching in the left or right subtrees. On average, this means that each comparison allows the operations to skip about half of the tree, so that each lookup, insertion or deletion takes time proportional to the logarithm of the number of items stored in the tree. This is much better than the linear time required to find items by key in an (unsorted) array, but slower than the corresponding operations on hash tables.

Frequently, the information represented by each node is a record rather than a single data element. However, for sequencing purposes, nodes are compared according to their keys rather than any part of their associated records. The major advantage of binary search trees over other data structures is that the related sorting algorithms and search algorithms such as in-order traversal can be very efficient; they are also easy to code.

Binary search trees are a fundamental data structure used to construct more abstract data structures such as sets, multisets, and associative arrays.

• When inserting or searching for an element in a binary search tree, the key of each visited node has to be compared with the key of the element to be inserted or found.
• The shape of the binary search tree depends entirely on the order of insertions and deletions, and can become degenerate.
• After a long intermixed sequence of random insertion and deletion, the expected height of the tree approaches square root of the number of keys, √n, which grows much faster than log n.
• There has been a lot of research to prevent degeneration of the tree resulting in worst case time complexity of O(n) (for details see section Types).

Binary search tree is a data structure that quickly allows us to maintain a sorted list of numbers.

• It is called a binary tree because each tree node has maximum of two children.
• It is called a search tree because it can be used to search for the presence of a number in O(log(n)) time.

The properties that separates a binary search tree from a regular binary tree is

1. All nodes of left subtree are less than root node
2. All nodes of right subtree are more than root node
3. Both subtrees of each node are also BSTs i.e. they have the above two properties

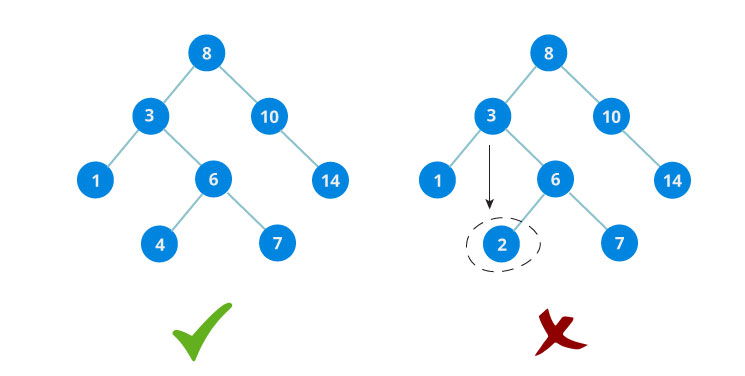
The binary tree on the right isn't a binary search tree because the right subtree of the node "3" contains a value smaller that it.

Source : https://www.programiz.com/dsa/binary-search-tree